Hace unas semanas os hablamos de nuestra participación en la tercera edición del European R Users Meeting (eRum 2018), una conferencia internacional que tiene como objetivo la transferencia de conocimiento y el encuentro entre usuarios profesionales del entorno de software libre y lenguaje de programación R[1], enfocado al análisis estadístico. Allí, nuestro trabajo Finding groups in time-to-event data by means of the clustcurv package[2], que permite agrupar curvas de supervivencia mediante técnicas de clustering o agrupación de manera automática, resultó galardonado con uno de los premios del congreso. El objetivo de este proyecto era configurar una herramienta útil para la toma de decisiones en las organizaciones que trabajan con un gran volumen de datos, como las pertenecientes a la Industria 4.0 o al sector de la banca.
A lo largo de este post hablaremos de las técnicas de clustering y de cómo aprovechar toda la información que pueden proporcionar para la toma de decisiones en cualquier proceso de negocio y para cualquier sector.
Curvas de supervivencia, análisis de tiempos y censoring
Conocer el tiempo de vida de un paciente tras el diagnóstico de una enfermedad, comparar diferentes tratamientos médicos para averiguar cuál produce una mayor tasa de supervivencia o identificar los factores de riesgo de una enfermedad son algunas de las cuestiones que llevaron al desarrollo de nuevas técnicas estadísticas conocidas bajo el nombre genérico de análisis de supervivencia, por su aplicación en el campo de la medicina.
En la actualidad, su uso se ha extendido a otros campos como el de la economía, la educación, la biología o la industria. Por ejemplo, para una entidad bancaria es de gran interés conocer el tiempo que pasa hasta que se produce el impago de un crédito o determinar el tiempo de vida de sus clientes y si este tiempo es similar para todas las regiones de un país. En el ámbito educativo, y debido al aumento del fracaso escolar en menores, es determinante conocer en qué momento un estudiante decide abandonar sus estudios y qué factores influyen en esta decisión. Para una empresa que incorpore un sistema de cadena de montaje en su producción, se podría determinar el tiempo de fallo de una pieza o el deterioro de un sistema para establecer los períodos de garantía de un producto o el diseño de planes de mantenimiento preventivo.
Sin importar el sector en el que se aplique, el análisis de supervivencia tiene como objetivo modelar el tiempo que transcurre hasta que ocurre un determinado evento o suceso (fallecimiento, enfermedad, impago de un crédito, fallo de un sistema, etc.), dando como resultado la estimación de curvas de supervivencia que nos permitirá sacar conclusiones. Su característica principal es que incorpora el fenómeno conocido como censura (censoring) que hace referencia a la presencia de observaciones con información incompleta (observaciones censuradas). Este fenómeno ocurre cuando tenemos información parcial sobre el tiempo hasta el evento porque no conocemos el momento exacto en el qué ocurrirá.
Pongamos el caso en el que se lleva a cabo un estudio piloto de seis meses de duración para analizar la efectividad de un nuevo método de producción de motores de barcos. Para ello es necesario medir el número de días que transcurren hasta que un motor falla. Durante estos seis meses observaremos motores que dejaron de funcionar, pero también es probable que algunos motores sigan funcionando al final del estudio. En estos casos, nos faltará información sobre la duración real de estos motores, sabemos cuántos días llevan funcionando pero no conocemos cuánto tiempo de vida útil les quedará. Para tratar este tipo de información incompleta se recurre al análisis de supervivencia.
Clustering, fundamental para la agrupación en machine learning
Dentro de las técnicas estadísticas o de machine learning es común hablar de aprendizaje supervisado y aprendizaje no supervisado.
Habitualmente, en el análisis de datos disponemos de una variable respuesta -u output si utilizamos el lenguaje de machine learning– que deseamos predecir en función de un conjunto de variables independientes o inputs. Es necesario recordar que la variable respuesta podría ser cuantitativa (como por ejemplo, el número de bytes enviados por un host) o cualitativa (como la etiqueta email o spam). Además, contaremos con un conjunto de datos de entrenamiento en los que observaremos tanto la variable respuesta como las distintas variables independientes en un conjunto de elementos (como los hosts dentro de una red o los correos electrónicos recibidos) y con toda esta información construiremos un modelo predictivo que nos permitirá conocer la variable respuesta para un elemento no visto.
El escenario previo describe lo que se conoce como aprendizaje supervisado y recibe este nombre porque la presencia de la variable respuesta guía o supervisa este aprendizaje. Por el contrario, en el aprendizaje no supervisado sólo observaremos las variables independientes y no tendremos registro alguno de la respuesta. En consecuencia nuestro objetivo en este contexto será describir cómo se organizan o agrupan los datos. Por este motivo, en este tipo de aprendizaje se usan mayoritariamente las técnicas de agrupamiento o clustering.
Llegado a este punto, si en algún momento surge la necesidad de agrupar datos con la particularidad de que éstos hagan referencia a tiempos hasta un determinado evento, una posible solución a esta tarea se basa en el uso del algoritmo desarrollado e implementado en clustcurv. Este algoritmo de aprendizaje no supervisado permite la agrupación de curvas de supervivencia, dando como resultado tanto la asignación de cada curva a su grupo como el número de grupos existentes. Es importante resaltar que esta última característica es la principal innovación de la herramienta y una ventaja para la toma de decisiones, ya que hasta el momento la elección del número de grupos se hacía según el criterio individual del profesional.
clustcurv, algoritmo inédito para la toma de decisiones
Supongamos que tenemos un modelo general de $\LARGE J$ muestras con censura aleatoria donde las observaciones provienen de $\LARGE n_j$ individuos de la población $\LARGE j(j=1, \ldots, n)$. Denotamos $\LARGE n = \sum_{j=1}^{J} n_j$ y asumimos que las observaciones de los $\LARGE n$ individuos son mutuamente independientes. Sea $\LARGE T_{ij}$ un tiempo al evento correspondiente a un evento medido desde el principio del estudio del $\LARGE i$-ésimo sujeto $\LARGE (i= 1, \ldots, n_j)$ en la muestra $\LARGE j$ y asumiendo que $\LARGE T_{ij}$ es observado sujeto a una variable aleatoria de censura (univariante) por la derecha $\LARGE C_{ij}$ que se asume independiente de $\LARGE T_{ij}$. Debido a la censura, en lugar de $\LARGE T_{ij}$, observamos $\LARGE (\tilde T_{ij}, \Delta_{ij})$ donde $\LARGE \tilde T_{ij}=\min(T_{ij}, C_{ij}), \Delta_{ij} = I(T_{ij} \le C_{ij})$ e $\LARGE I(\cdot)$ es la función indicadora.
De manera general, el procedimiento propuesto por Villanueva, Sestelo y Meira-Machado en Statistics in Medicine[3], nos permitirá determinar grupos de curvas de supervivencia. Formalmente esto sería, comprobar si los $\LARGE 1, \ldots, J$ niveles pueden ser agrupados en $\LARGE K$ grupos $\LARGE (G_1, \ldots, G_K)$ con $\LARGE K < J$, tal que $\LARGE S_i = S_j$ para todo $\LARGE i, j \in G_k$, para todo $\LARGE k=1, \ldots, K$. Brevemente, los pasos de este algoritmo son los siguientes:
- Se estiman las curvas de supervivencia $\LARGE S_j(t) = P(T_j > t)$. Éstas pueden ser consistentemente estimadas usando el estimador no paramétrico Kaplan-Meier[4] con base en $\LARGE (\tilde T_j, \Delta_j)$. El estimador Kaplan-Meier, también conocido como el estimador del producto límite, es el método más frecuentemente utilizado para estimar supervivencia en presencia de censura. Siendo $\LARGE t_1 < t_2 < \ldots < t_{m_j}, m_j\le n_j$ los distintos tiempos de fallo ordenados de la población $\LARGE j (j = 1, \ldots, J)$ y $\LARGE d_u$ el número de eventos de la población $\LARGE j$ en tiempo $\LARGE t_u$, el estimador Kaplan-Meier de la función de supervivencia (para la población $\LARGE j$) se define como$$\LARGE \widehat S_j(t) = \prod_{u:t_u\leq t} \left(1-\frac{d_u}{R_j(t_u)}\right)$$donde $\LARGE R_j(t) = \sum_{i=1}^{n_j} I(\tilde T_{ij} \le t)$ denota el número de individuos en riesgo justo antes del tiempo $\LARGE t$.
- Dado un número de grupos $\LARGE K$, se utiliza el algoritmo k-means[5] con base en la distancia $\LARGE L_2$ o el k-medians[6] con base en la $\LARGE L_1$ sobre las estimaciones anteriores para obtener la “mejor” partición $\LARGE (G_1, \ldots, G_K)$.
- A continuación, mediante un procedimiento basado en bootstrap[7],[8], se contrasta la hipótesis nula $\LARGE H_0(K)$ de que existen $\LARGE K$ grupos de curvas.
- Se repiten los pasos 2 y 3 desde $\LARGE K=1$ hacia delante hasta que una cierta hipótesis nula sea aceptada. Así, el número $\LARGE K$ de grupos será determinado.
Esta metodología está actualmente implementada en un paquete de R (clustcurv), disponible como software libre a disposición de todo aquel que lo necesite (comunidad científica, otras organizaciones, empresas, etc.).
Cómo aplicar este algoritmo: un caso real
Para ilustrar el funcionamiento de la metodología desarrollada se muestra un pequeño ejemplo utilizando datos reales de pacientes con cáncer de colon[9]. Para hacernos una idea del tipo de datos disponibles, se muestra un ejemplo en la Figura 1 en la que se representan cuatro individuos que forman parte de un estudio médico, a los que se les realizó un seguimiento hasta la finalización del mismo o hasta el momento en que tuvo lugar el fallecimiento (evento). Se puede observar cómo dos de los individuos fallecen antes de que acabe el estudio, mientras que en los otros casos el evento no ha tenido lugar. Es por este motivo que los datos se denominan “censurados” ya que proporcionan información parcial, es decir, sabemos que estos individuos han sobrevivido a la duración del estudio pero desconocemos cuántos días de vida les quedan.
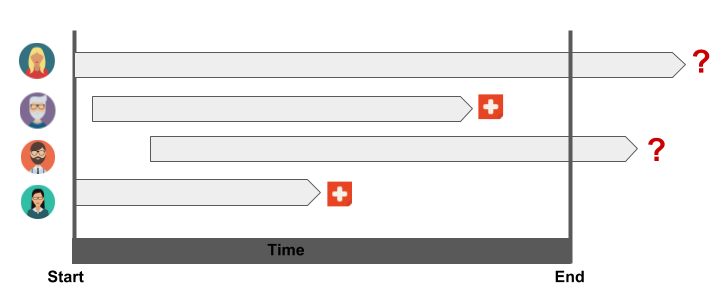
Figura 1. Ilustración de la censura
La base de datos consta de información recogida de 929 sujetos que fueron operados para eliminar cualquier resto de tumor. El conjunto de datos está disponible como parte del paquete de R condSURV[10],[11]. De los 929 sujetos, 452 fallecieron transcurrido un tiempo después de la operación, por lo que tendremos observaciones completas y otras observaciones censuradas con información parcial sobre sus tiempos de vida.
A través de la herramienta propuesta se puede llevar a cabo el análisis de datos.
devtools::install_github("noramvillanueva/clustcurv")
library(clustcurv)
library(survival)
library(condSURV)
colonCSm <- na.omit(data.frame(time = colonCS$Stime, status = colonCS$event,
nodes = colonCS$nodes))
# deleting people with zero nodes
colonCSm <- colonCSm[-c(which(colonCSm$nodes == 0)), ]
# grouping people with more than 10 nodes
colonCSm$nodes[colonCSm$nodes >= 10] <- 10
table(colonCSm$nodes) # 10 levels
## 1 2 3 4 5 6 7 8 9 10
## 274 194 125 84 46 43 38 23 20 62
head(colonCSm)
## time status nodes
## 1 1521 1 5
## 2 3087 0 1
## 3 963 1 7
## 4 293 1 6
## 5 659 1 10
## 6 1767 1 9
En la salida del código anterior, se observa –para cada paciente– la variable time (tiempo en días hasta el fallecimiento desde la entrada en el estudio), la variable status que es un indicador del estado vital al final del estudio (censurado o no), y una covariable nodes que indica el número de nodos linfáticos detectados con cáncer (agrupados de 1 a $\LARGE \ge$ 10).
Las curvas de supervivencia estimadas después de dividir los datos teniendo en cuenta el número de nodos se representan en la Figura 2. Cada una de las curvas muestra la probabilidad de que una persona con $\LARGE 1, \ldots, \le 10$ nodos sobreviva a tiempo $\LARGE t$.
model <- survfit(Surv(time, status) ~ factor(nodes), data = colonCSm) autoplot(model, conf.int = FALSE)
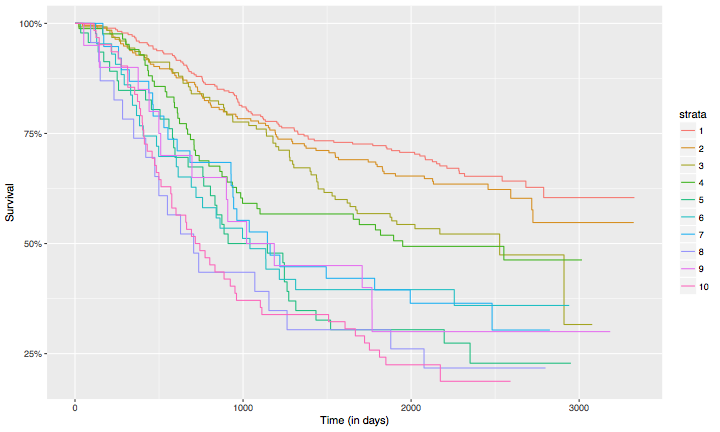Figura 2. Curvas de supervivencia estimadas para cada uno de los niveles de la variable nodes utilizando el estimador Kaplan-Meier
Cuando nos encontramos con un conjunto de datos como estos, con una variable categórica con un número elevado de niveles, quizás una buena aproximación sea la de establecer grupos con el mismo riesgo o probabilidad de supervivencia. Para llevar a cabo esta tarea, la única opción hasta el momento es aplicar primero un test tipo Log-rank[12] donde la hipótesis nula que se contrasta es la igualdad de curvas de supervivencia, y si el test resulta estadisticamente significativo, hacer un análisis post hoc de comparaciones por pares. El código y los p-valores obtenidos después de aplicar dicho test y las comparaciones dos a dos se muestran a continuación:
survdiff(Surv(time, status) ~ factor(nodes), data = colonCSm) # log-rank test ## Call: ## survdiff(formula = Surv(time, status) ~ factor(nodes), data = colonCSm) ## ## N Observed Expected (O-E)^2/E (O-E)^2/V ## factor(nodes)=1 274 94 151.93 22.0901 33.9249 ## factor(nodes)=2 194 74 102.87 8.1022 10.5979 ## factor(nodes)=3 125 61 62.56 0.0387 0.0453 ## factor(nodes)=4 84 43 38.26 0.5868 0.6434 ## factor(nodes)=5 46 34 17.06 16.8249 17.5428 ## factor(nodes)=6 43 27 16.43 6.8027 7.0736 ## factor(nodes)=7 38 25 15.41 5.9636 6.1880 ## factor(nodes)=8 23 18 7.22 16.0875 16.3765 ## factor(nodes)=9 20 14 8.05 4.3931 4.4795 ## factor(nodes)=10 62 49 19.21 46.2239 48.6066 ## ## Chisq= 129 on 9 degrees of freedom, p= 0 survminer::pairwise_survdiff(Surv(time, status) ~ nodes, data = colonCSm, p.adjust.method = "BH") ## ## Pairwise comparisons using Log-Rank test ## ## data: colonCSm and nodes ## ## 1 2 3 4 5 6 7 8 9 ## 2 0.41644 - - - - - - - - ## 3 0.00853 0.10482 - - - - - - - ## 4 0.00221 0.04032 0.51450 - - - - - - ## 5 3.9e-09 1.8e-06 0.00072 0.03427 - - - - - ## 6 1.7e-05 0.00072 0.03750 0.22540 0.60307 - - - - ## 7 2.1e-05 0.00072 0.04219 0.25752 0.49274 0.95088 - - - ## 8 3.0e-08 4.1e-06 0.00047 0.01407 0.51450 0.30796 0.25752 - - ## 9 0.00043 0.00493 0.08152 0.23872 0.76034 0.90717 0.79064 0.51450 - ## 10 < 2e-16 1.2e-11 9.1e-07 0.00047 0.37154 0.16671 0.10386 0.95088 0.37007 ## ## P value adjustment method: BH
Teniendo en cuenta estas salidas numéricas, la interpretación parece no ser inmediata, por lo que la toma de decisiones por parte del usuario final o el médico resulta bastante compleja. Llegado a este punto, lo más fácil es aplicar el algoritmo propuesto. Para un nivel de significación de 0.05, la hipótesis nula $\LARGE H_0(1)$ es rechazada (p-valor < 0.01) mientras que la hipótesis nula $\LARGE H_0(2)$ es aceptada (p-valor de 0.18).
res <- clustcurv_surv(time = colonCSm$time, status = colonCSm$status, fac = colonCSm$nodes, algorithm = "kmeans", nboot = 100, cluster = TRUE, seed = 300716) ## Checking 1 cluster... ## Checking 2 clusters... ## ## Finally, there are 2 clusters. res$table ## H0 Tvalue pvalue ## 1 1 15.425589 0.00 ## 2 2 2.364531 0.18
La asignación de las curvas a los dos grupos resultantes puede observarse en la Figura 3. Es importante destacar que tener cinco o más nodos linfáticos con presencia de cáncer parece estar relacionado con una menor supervivencia que tener cuatro o menos (grupo 1: $\LARGE \le$4 nodos, grupo 2: $\LARGE >$4 nodos).
autoplot(res, groups_by_colour = TRUE, xlab = "Time (in days)")
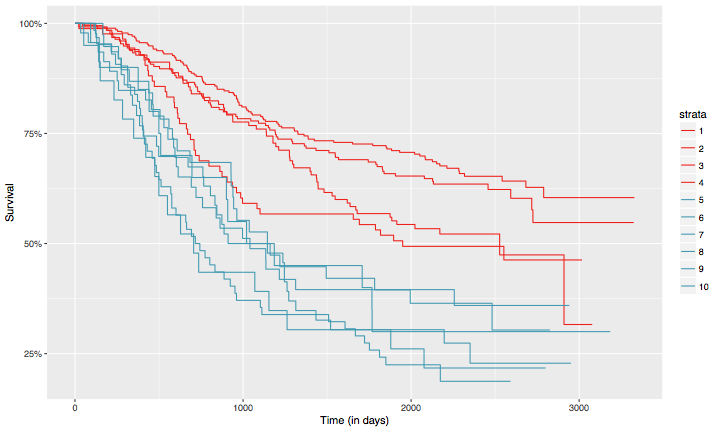
Figura 3. Curvas de supervivencia estimadas para cada uno de los niveles de la variable “nodos”. Un color específico se asigna a cada curva de acuerdo al grupo al que pertenece (en este caso dos grupos, $\LARGE K = 2$)
Otros ejemplos dentro del análisis de supervivencia aplicado en este caso al sector financiero pueden consultarse en el libro A short course on Survival Analysis applied to the Financial Industry, publicado por Marta Sestelo en 2017[13].
El paquete clustcurv está ya disponible en el CRAN (Comprehensive R Archive Network). Puedes acceder a través de este enlace: https://cran.r-project.org/web/packages/clustcurv/index.html
Referencias
[1] R Core Team (2018). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL: http://www.R-project.org/.
[2] Villanueva, N.M., Sestelo, M. and Meira-Machado, L. (2019). clustcurv: Determining Groups in Multiples Curves. R package version 1.0.0, 2019. URL: http:
[3] Villanueva, N.M., Sestelo, M. and Meira-Machado, L. (2019). A Method for Determining Groups in Multiple Survival Curves. Statistics in Medicine, 38:866–877. URL: https://onlinelibrary.wiley.com/doi/10.1002/sim.8016
[4] Kaplan, E.L., and Meier, P. (1958). Nonparametric Estimation from Incomplete Observations. Journal of the American Statistical Association, 53: 457–81.
[5] Macqueen, J.B. (1967). Some methods of classification and analysis of multivariate observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, University of California Press, 281-297.
[6] Kaufman, L. and Rousseeuw, P. J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis. John Wiley.
[7] Efron, B. (1979). Bootstrap methods: another look at the jackknife. The Annals of Statistics, 7: 1-26.
[8] Efron, B. (1981). Censored Data and the Bootstrap. Journal of the American Statistical Association, 76(374): 312-319.
[9] Moertel, C.G., Fleming, T.R., Macdonald, J.S., Haller, D.G., Laurie, J.A., Goodman, P.J., Ungerleider, J.S., Emerson, W.A., Tormey, D.C., Glick, J.H. et al. (1990). Levamisole and fluorouracil for adjuvant therapy of resected colon carcinoma. New England Journal of Medicine, 322(6): 352–358.
[10] Meira-Machado, L., Sestelo, M. (2016). condSURV: Estimation of the Conditional Survival Function for Ordered Multivariate Failure Time Data. R package, version 2.0.1.
[11] Meira-Machado, L. and Sestelo, M. (2016). condSURV: An R Package for the Estimation of the Conditional Survival Function for Ordered Multivariate Failure Time Data. The R Journal, 8(2): 460-473.
[12] Mantel, N. (1966). Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemotherapy Reports, 50(3): 163–170.
[13] Sestelo, M (2017). A short course on Survival Analysis applied to the Financial Industry. BBVA Data & Analytics, Madrid. https://bookdown.org/sestelo/sa_financial/
Autoras: Nora M. Villanueva, investigadora y desarrolladora senior del área de Servicios y Aplicaciones y Marta Sestelo, investigadora y desarrolladora senior en el área de Sistemas Inteligentes en Red (INetS) de Gradiant
